Khái niệm đạo hàm trong toán học giải tích không chỉ giới hạn ở việc xác định tốc độ thay đổi của một số . Công thức đạo hàm cấp cao, một công cụ mạnh mẽ giúp khám phá sâu hơn về bản chất của hàm số, giúp chúng tôi giải quyết các bài toán phức tạp một cách hiệu quả. Trong bài viết này, chúng tôi sẽ đi sâu vào công thức đạo hàm cấp cao, ứng dụng, các dạng bài tập liên quan, so sánh với đạo hàm bình thường, sử dụng giải tích và cuối cùng là các ví dụ minh họa cụ thể .
1. Giới thiệu về công thức đạo hàm cấp cao
Công thức đạo hàm cấp cao là một thông tin mở rộng thông thường của khái niệm đạo hàm. Chúng ta không chỉ có thể tính đạo chức năng cấp một mà còn có thể tính đạo chức năng cấp hai, cấp ba và như vậy đến bất kỳ cấp nào khác.
Đạo hàm bậc hai và ý nghĩa hình học
- để mở rộng ra các đạo hàm cấp cao hơn, chẳng hạn như các đạo hàm bậc ba, bậc bốn,… Đạo hàm cấp n của hàm số f(x), có ký hiệu là f^(n)(x), và đạo hàm cấp (n-1) của đạo hàm f(x).
- bậc ba f”'(x) là tốc độ thay đổi của gia tốc, đạo hàm bậc bốn f^(4)(x) là tốc độ thay đổi của tốc độ thay đổi gia tốc, và v.v.
Định nghĩa tổng quát về đạo hàm cấp cao
- Có một số quy tắc thường được sử dụng trong việc ký hiệu đạo hàm cấp cao để giảm nhầm lẫn và tăng tính rõ ràng. Ký hiệu f”(x), f”'(x) thường được sử dụng cho các bậc đạo hàm bậc thấp như bậc hai và bậc ba. hoặc d2y/dx2, d3y/dx3, và vv
- Nhưng bậc đạo hàm quá lớn khiến việc viết như vậy trở nên khó khăn. Do đó, để biểu diễn hàm cấp n, người ta thường sử dụng ký hiệu f^(n)(x) hoặc d^ny/dx^n.
Ký hiệu và các quy ước về đạo hàm cấp cao
- Công thức đạo hàm cấp cao không chỉ là một khái niệm trừu tượng mà còn là một phương pháp mạnh mẽ có nhiều ứng dụng thực tế trong tính toán. Đạo hàm cấp cao rất quan trọng trong nhiều lĩnh vực khoa học và kỹ thuật, từ việc xử lý các bài toán tối ưu hóa đến việc xác định giá trị của hàm số.
- Khả năng nắm vững và áp dụng các công thức này là rất quan trọng đối với bất kỳ ai muốn tiến sâu vào các lĩnh vực đòi hỏi tư duy toán học cao.

2. Ứng dụng của công thức đạo hàm cấp cao trong tính toán
Xây dựng chuỗi Taylor và Maclaurin là một trong những sử dụng quan trọng nhất của đạo hàm cấp cao. Chuỗi Taylor mô tả hàm số như một tổng vô hạn các số hạng. Trong chuỗi Taylor, mỗi số hạng bao gồm một đạo hàm cấp cao của hàm số tại một thời điểm nhất định, được nhân với một lũy thừa của hiệu số (x-a) và sau đó chia cho giai thừa Chuỗi Maclaurin là một ví dụ về chuỗi Taylor khi a=0.
Tính toán chuỗi Taylor và Maclaurin
- Đạo hàm cấp cao đóng một vai trò quan trọng trong việc xác định các điểm cực trị của hàm số trong các bài toán tối ưu hóa. Đạo hàm bậc hai hỗ trợ xác định các điểm dừng (nơi đạo hàm bằng 0), trong khi đạo hàm bậc nhất hỗ trợ phân biệt giữa các điểm dừng là điểm cực đại, điểm cực tiểu hoặc điểm uốn.
- Cụ thể, nếu đạo hàm bậc hai f”(a) lớn hơn 0, thì a là điểm cực tiểu địa phương và điểm cực đại địa phương nếu f”(a) thấp hơn 0. Để đạt được kết luận, chúng ta phải xem xét các đạo hàm bậc cao hơn trong trường hợp f”(a) = 0.
Giải quyết các bài toán tối ưu hóa
- Đạo hàm cấp cao có rất nhiều ứng dụng ngoài toán học trong các lĩnh vực vật lý và kỹ thuật. Gia tốc, một khái niệm cơ học quan trọng, là đạo hàm bậc hai của quãng đường theo thời gian.
- Nhưng thường xuyên hơn không, các đạo hàm cấp cao hơn sẽ được sử dụng để mô tả các hiện tượng vật lý phức tạp hơn như sóng, dao động và các chuyển động không quán tính.
Các dạng bài tập liên quan đến công thức đạo hàm cấp cao
- Các bài tập sử dụng công thức đạo hàm cấp cao rất đa dạng và thường có độ khó cao hơn so với các bài tập đạo hàm thông thường.
- Chúng không chỉ đòi hỏi kiến thức cơ bản về đạo hàm mà còn đòi hỏi sự linh hoạt, phân tích vấn đề và tư duy logic. Do đó, việc luyện tập thường xuyên các dạng bài tập này là rất quan trọng để cải thiện khả năng toán học của bạn.
3. Bài tập tính đạo hàm cấp n của hàm số cơ bản
Tính đạo hàm cấp n của các hàm số đơn giản như hàm logarit, hàm đa thức, hàm lượng giác và hàm mũ là một trong những dạng bài tập cơ bản liên quan đến đạo hàm cấp cao. Các bài tập này không chỉ tăng cường khả năng tính toán và tư duy mà còn giúp chúng ta nắm vững các quy tắc đạo hàm. Để giải quyết các bài tập này, chúng ta thường phải tìm ra một quy luật chung khi sử dụng đạo hàm nhiều lần hoặc sử dụng các công thức đạo hàm đặc biệt.
Bài tập sử dụng công thức Leibniz
- Công thức Leibniz hỗ trợ tính đạo hàm cấp n của tích hai hàm số. Có thể tìm thấy công thức sau: (uv)(n) = Σ(k=0,n) C(n,k) là Trong trường hợp này, C(n,k) là hệ số nhị thức, u^(n-k) là đạo hàm cấp (n-k) của u và v^(k) là đạo hàm cấp k của v. Khi chúng ta gặp bài toán tính đạo hàm cấp n của một tích mà không thể tách thành các hàm số đơn giản hơn, công thức Leibniz thường được sử dụng.
- Công thức Leibniz có vẻ phức tạp khi sử dụng, nhưng thực tế là nó rất hiệu quả trong nhiều tình huống. Thông thường, các bài tập dạng này yêu cầu xác định rõ ràng các hàm u và v, tính đạo hàm của chúng cho đến bậc cần thiết, và sau đó áp dụng công thức cẩn thận để có được kết quả cuối cùng. Bên cạnh việc cải thiện kỹ năng tính toán của chúng ta, bài tập này cũng giúp chúng ta hiểu rõ hơn về cách công thức Leibniz được thiết kế.
Các bài toán ứng dụng chuỗi Taylor và Maclaurin
- Các bài toán sử dụng chuỗi Taylor và Maclaurin thường tìm giới hạn, xấp xỉ giá trị và phân tích tính chất của hàm số.
- Thông thường, các bài tập này yêu cầu sự hiểu biết sâu sắc về các công thức tính đạo hàm cấp cao, tính hội tụ và chuỗi. Điều quan trọng là phải xác định hàm, điểm và hạng cần thiết để đạt được độ chính xác mong muốn.
Bài tập liên quan đến các ứng dụng thực tế
- Giải các bài toán tối ưu hóa, giải các phương trình vi phân hoặc phân tích các hiện tượng vật lý và kỹ thuật là những ví dụ về các nhiệm vụ liên quan đến các ứng dụng thực tế của đạo hàm cấp cao.
- Để giải quyết các bài tập này, chúng ta không chỉ phải nắm vững công thức đạo hàm cấp cao mà còn phải có kiến thức về các lĩnh vực liên quan.
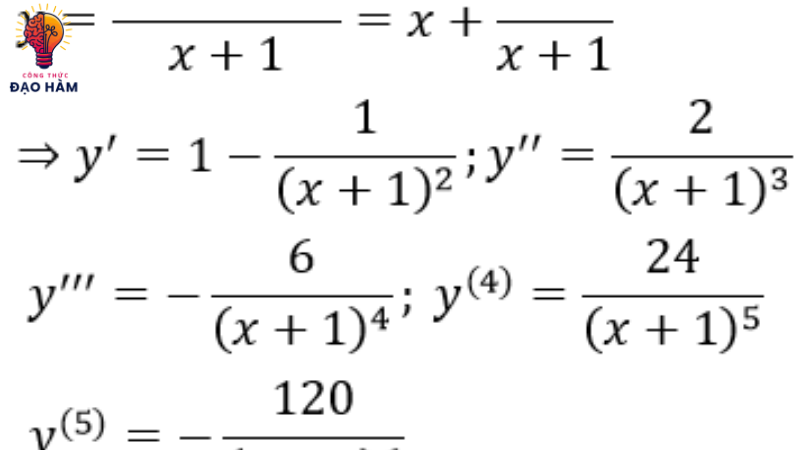
4. So sánh công thức đạo hàm cấp cao với đạo hàm thường
Việc so sánh công thức đạo hàm cấp cao với đạo hàm thường giúp chúng ta hiểu rõ hơn về ý nghĩa và bản chất của mỗi khái niệm. Đạo hàm thường, còn được gọi là đạo hàm bậc một, cho biết tốc độ mà một hàm số thay đổi tại một thời điểm cụ thể. Tuy nhiên, thông tin về sự thay đổi của tốc độ thay đổi đó lại được cung cấp bởi đạo hàm cấp cao, và điều này tiếp tục ở các cấp độ cao hơn.
Sự khác biệt về khái niệm và ý nghĩa
- Đạo hàm cấp cao và đạo hàm thường khác nhau về ý nghĩa. Độ dốc của đường cong của hàm số y=f(x) tại điểm x được xác định bởi đạo hàm bậc nhất, f'(x). Nó hiển thị tốc độ thay đổi của y so với x. Ví dụ, trong vật lý, vận tốc là đạo hàm của quãng đường theo thời gian.
- Độ cong của đường cong tại x, hoặc tốc độ thay đổi của độ dốc, được xác định bởi đạo hàm bậc hai f(x). Gia tốc trong vật lý là đạo hàm cấp hai của quãng đường theo thời gian.
Ứng dụng cụ thể của đạo hàm cấp cao mà đạo hàm thường không thể thay thế
- Mặc dù đạo hàm thường có lợi trong tìm cực trị và tìm tiếp tuyến, nhưng đạo hàm cấp cao có một số ứng dụng mà đạo hàm thường không thể thay thế được.
- Ví dụ, chúng ta phải xem xét dấu của đạo hàm bậc hai khi tìm các điểm uốn trên đồ thị hàm số. Điểm uốn là khi đồ thị hàm số chuyển từ lõm xuống sang lõm lên hoặc ngược lại.
Trường hợp nào cần sử dụng đạo hàm cấp cao?
- Đạo hàm thường là đủ để giải quyết vấn đề. Nhưng đạo hàm cấp cao là không thể thiếu trong một số trường hợp. Đạo hàm cấp cao là một công cụ cần thiết trong những trường hợp chúng ta cần phân tích độ cong của đồ thị hàm số, tìm các điểm uốn hoặc xấp xỉ hàm số bằng chuỗi Taylor.
5. Cách sử dụng công thức đạo hàm cấp cao trong giải tích
Trong giải tích, việc sử dụng công thức đạo hàm cấp cao đòi hỏi phải có sự hiểu biết sâu sắc về các quy tắc đạo hàm, khả năng phân tích vấn đề và sự linh hoạt. Chúng ta không chỉ biết cách tính toán đạo hàm mà còn biết cách sử dụng chúng để khám phá các tính chất của hàm số và giải quyết các bài toán phức tạp. Phần này sẽ đi sâu vào các yếu tố này và cung cấp cho người đọc một cái nhìn toàn diện về cách sử dụng công thức đạo hàm cấp cao trong giải tích.
- Các quy tắc đạo hàm cấp cao cơ bản: Các quy tắc đạo hàm cơ bản như tổng, hiệu, tích, thương và hàm hợp cũng được sử dụng để tính đạo hàm cấp cao. Nhưng để xác định đạo hàm của đạo hàm, chúng ta phải áp dụng các quy tắc này nhiều lần. Điều này đòi hỏi sự cẩn thận và kiên nhẫn khi tính toán. Ngoài ra, kiến thức cơ bản về các quy tắc đạo hàm cơ bản là cần thiết để tính đạo hàm cấp cao chính xác.
- Kỹ năng phân tích hàm số để áp dụng công thức đạo hàm cấp cao: Khả năng phân tích hàm số là một trong những kỹ năng quan trọng nhất khi sử dụng công thức đạo hàm cấp cao. Để lựa chọn phương pháp tính đạo hàm phù hợp, chúng ta phải xác định cấu trúc của hàm số, bao gồm các hàm thành phần, các phép toán và các hằng số. Kỹ năng phân tích không chỉ giúp chúng ta xác định công thức phù hợp mà còn giúp chúng ta thực hiện những hành động hiệu quả và hợp lý.
- Vận dụng các công thức đạo hàm cấp cao trong các bài toán thực tế: Khả năng kết hợp kiến thức toán học với kiến thức trong các lĩnh vực khác, chẳng hạn như vật lý, kỹ thuật, khoa học máy tính và kinh tế, là cần thiết để sử dụng các công thức đạo hàm cấp cao trong các bài toán thực tế. Chúng ta không chỉ phải tính đạo hàm trong các bài toán này; chúng ta cũng cần hiểu cách sử dụng đạo hàm để mô tả, phân tích và giải quyết các vấn đề thực tế.
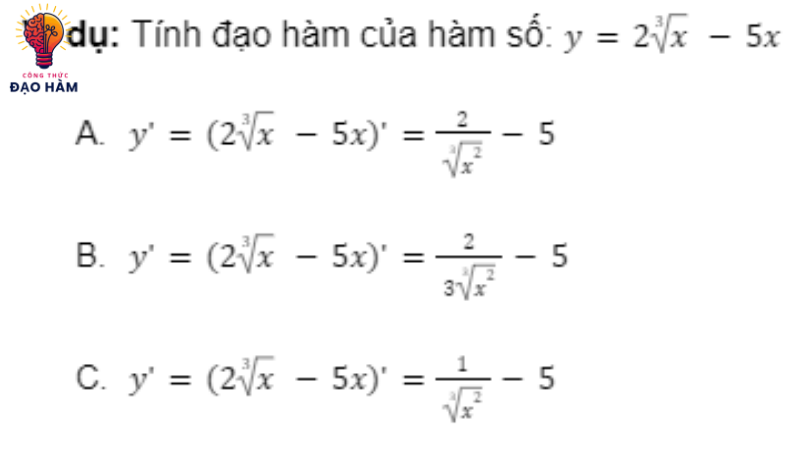
6. Ví dụ minh họa công thức đạo hàm cấp cao
Chúng ta sẽ xem ba ví dụ cụ thể để làm rõ hơn về công thức đạo hàm cấp cao và cách chúng được sử dụng. Bài tập liên quan đến việc áp dụng các công thức chuỗi Taylor và Leibniz đến việc xác định đạo hàm của các hàm số đơn giản sẽ được trình bày trong các ví dụ này. Các ví dụ này sẽ cho chúng ta một cái nhìn rõ ràng hơn về sức mạnh và tính ứng dụng của đạo hàm cấp cao.
Ví dụ 1: Tính đạo hàm cấp n của hàm số e^x*sin(x)
- Chúng ta sẽ tính đạo hàm cấp n của hàm số f(x) = e^x*sin(x) trong ví dụ này. Đây là một ví dụ về cách sử dụng công thức Leibniz để tính đạo hàm cấp cao của tích hai hàm số. Các hàm số u và v trong tích e^x*sin(x), tức là u = e^x và v = sin(x), phải được xác định rõ ràng để áp dụng công thức Leibniz một cách hiệu quả.
Ví dụ 2: Tìm chuỗi Maclaurin của hàm số ln(1+x)
- Ví dụ thứ hai cho thấy đạo hàm cấp cao được sử dụng để tìm chuỗi Maclaurin của hàm số ln(1+x). Chuỗi Maclaurin, một trường hợp của chuỗi Taylor, có điểm khai triển là x=0. Đạo hàm cấp n của hàm số ln(1+x) phải được tìm thấy tại x=0. Sau đó, chúng ta sẽ sử dụng công thức chuỗi Maclaurin để tìm biểu thức khai triển.
Ví dụ 3: Ứng dụng đạo hàm cấp cao trong vật lý
- Đạo hàm cấp cao được sử dụng trong vật lý, đặc biệt là trong bài toán phân tích chuyển động, như thể hiện trong ví dụ thứ ba này. Giả sử một chất điểm đi trên một đường thẳng, với quãng đường s(t) là hàm số thời gian t. Vận tốc v(t) và gia tốc a(t) là hai đạo hàm bậc nhất của s(t) theo t. Nhiều khi, gia tốc là một hàm số của thời gian thay Vì là một hằng số nên điều này có nghĩa là chúng ta phải sử dụng đạo hàm bậc ba.
7. Kết luận
Trong toán học giải tích, ý tưởng về công thức đạo hàm cấp cao là một khái niệm quan trọng. Nó là sự mở rộng của đạo hàm thông thường và là một công cụ mạnh mẽ có nhiều ứng dụng thực tế. Đạo hàm cấp cao là cần thiết trong nhiều lĩnh vực khoa học và kỹ thuật, từ công việc tính toán chuỗi Taylor và Maclaurin để giải quyết các bài toán tối ưu hóa.
Tóm lại, công thức đạo hàm cấp cao là một công cụ quan trọng giúp phân tích và giải quyết nhiều vấn đề trong toán học và ứng dụng thực tiễn. Hiểu rõ cách áp dụng công thức này không chỉ nâng cao kỹ năng giải toán mà còn hỗ trợ các lĩnh vực khoa học kỹ thuật và kinh tế. Cũng giống như việc kiểm soát bệnh hen suyễn đòi hỏi sự kiên trì và phương pháp phù hợp, việc nắm vững đạo hàm cấp cao cũng cần sự rèn luyện và tư duy hệ thống, chi tiết xin truy cập website congthucdaoham.com xin cảm ơn!

